Bài 4: Hàm số lượng giác và đồ thị

I. Hàm số chẵn, hàm số lẻ

1. Hàm số chẵn:

Ví dụ: Hàm số $f(x)=\dfrac{x^2}{4}$ là hàm số chẵn vì
+) TXĐ: $\mathbb D =\mathbb R$ (thoả mãn (1)).
+) $f(-x)=\dfrac{(-x)^2}{4}=\dfrac{x^2}{4}=f(x)$ (thoả mãn (2)).

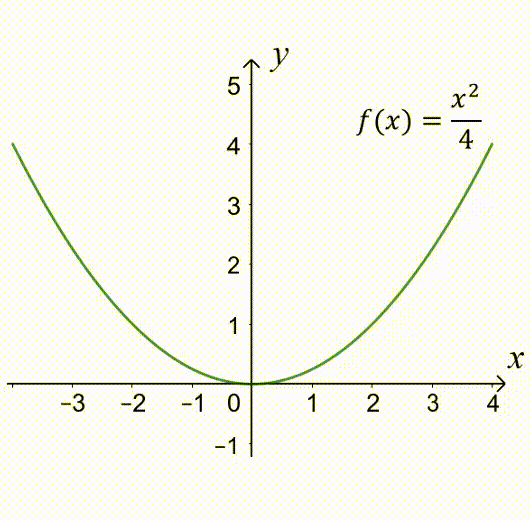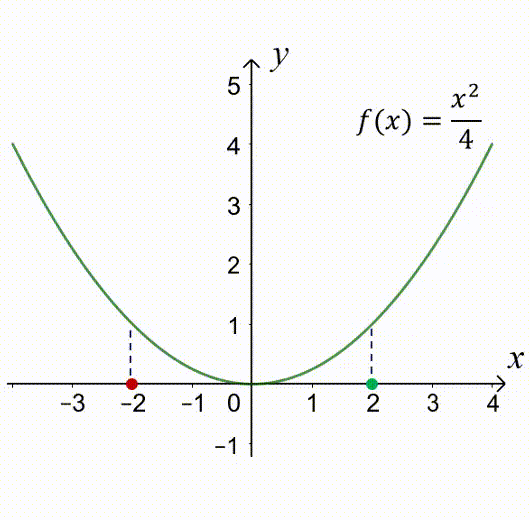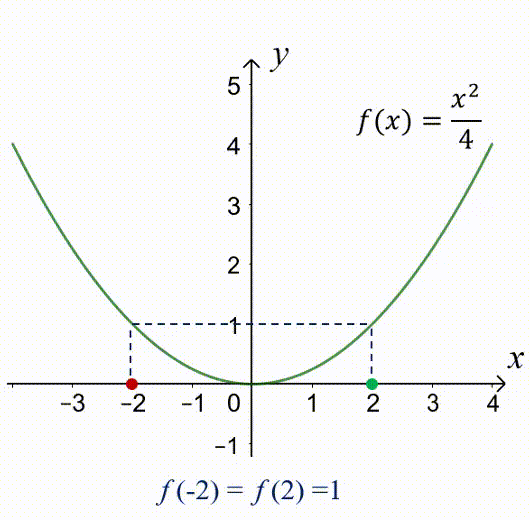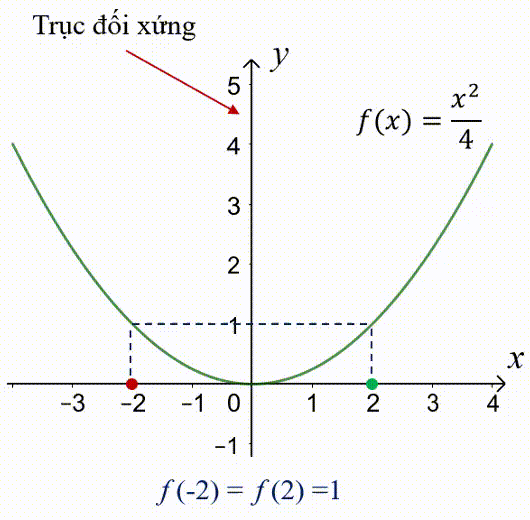
Nhận xét: đồ thị của hàm số chẵn $f(x)=\dfrac{x^2}{4}$ đối xứng qua trục tung $Oy$.

Tổng quát: Đồ thị của hàm số chẵn đối xứng qua trục tung.

Space

2. Hàm số lẻ:

Ví dụ: Hàm số $f(x)=2x$ là hàm số lẻ vì
+) TXĐ: $\mathbb D =\mathbb R$ (thoả mãn (3)).
+) $f(-x)=2.(-x)=-2x=-f(x)$. (thoả mãn (4)).

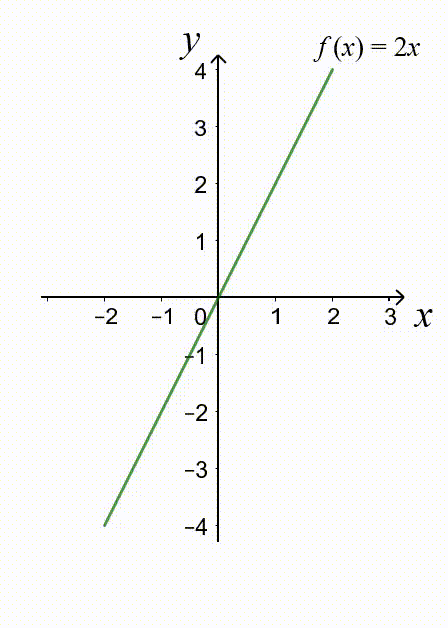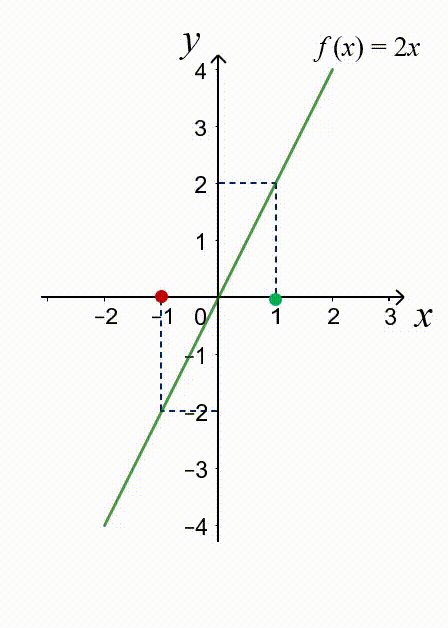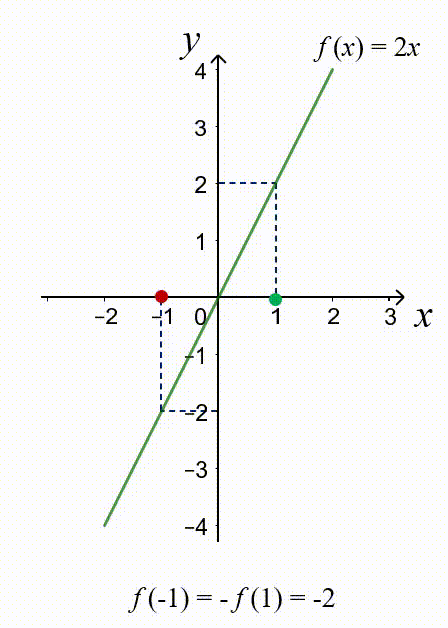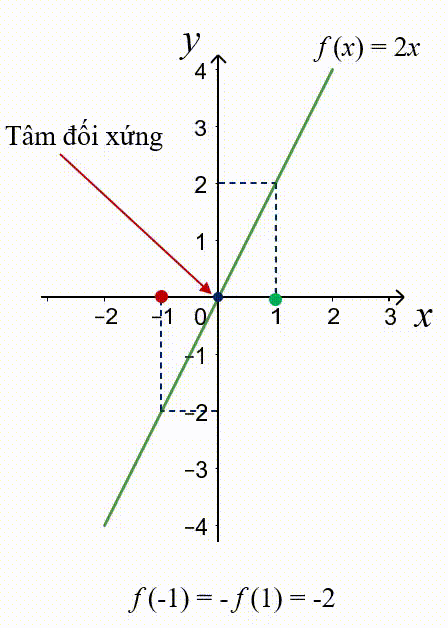
Nhận xét: đồ thị của hàm số lẻ $f(x)=2x$ có tâm đối xứng là $O(0;0)$.

Tổng quát: Đồ thị của hàm số chẵn đối xứng qua gốc toạ độ $O(0;0)$.

Space

II. Hàm số tuần hoàn

Hàm số $y=f(x)$ có tập xác định $\mathbb D$ được gọi là hàm số tuần hoàn nếu tồn tại một số $T \neq 0$ sao cho với mọi $x \in \mathbb D$, ta có:

+) $x+T\in \mathbb D$ và $x-T\in \mathbb D$;

+) $f(x+T)=f(x)$.

Số dương $T$ nhỏ nhất thoả mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.

Ví dụ: Đồ thị dưới đây là của hàm số tuần hoàn với chu kì $1$:

Giá trị của hàm số này bằng nhau tại các điểm có khoảng cách bằng $1$.

Tổng quát: Muốn vẽ đồ thị của một hàm số tuần hoàn chu kì $T$, ta chỉ cần vẽ đồ thị trên một đoạn có độ dài bằng $T$, sau đó dịch chuyển song song sang phải sang trái các đoạn lân cận cũng có độ dài bằng $T$.

(Phần vẽ đồ thị sẽ được giải thích rõ ở trong các phần đồ thị của hàm số lượng giác.)