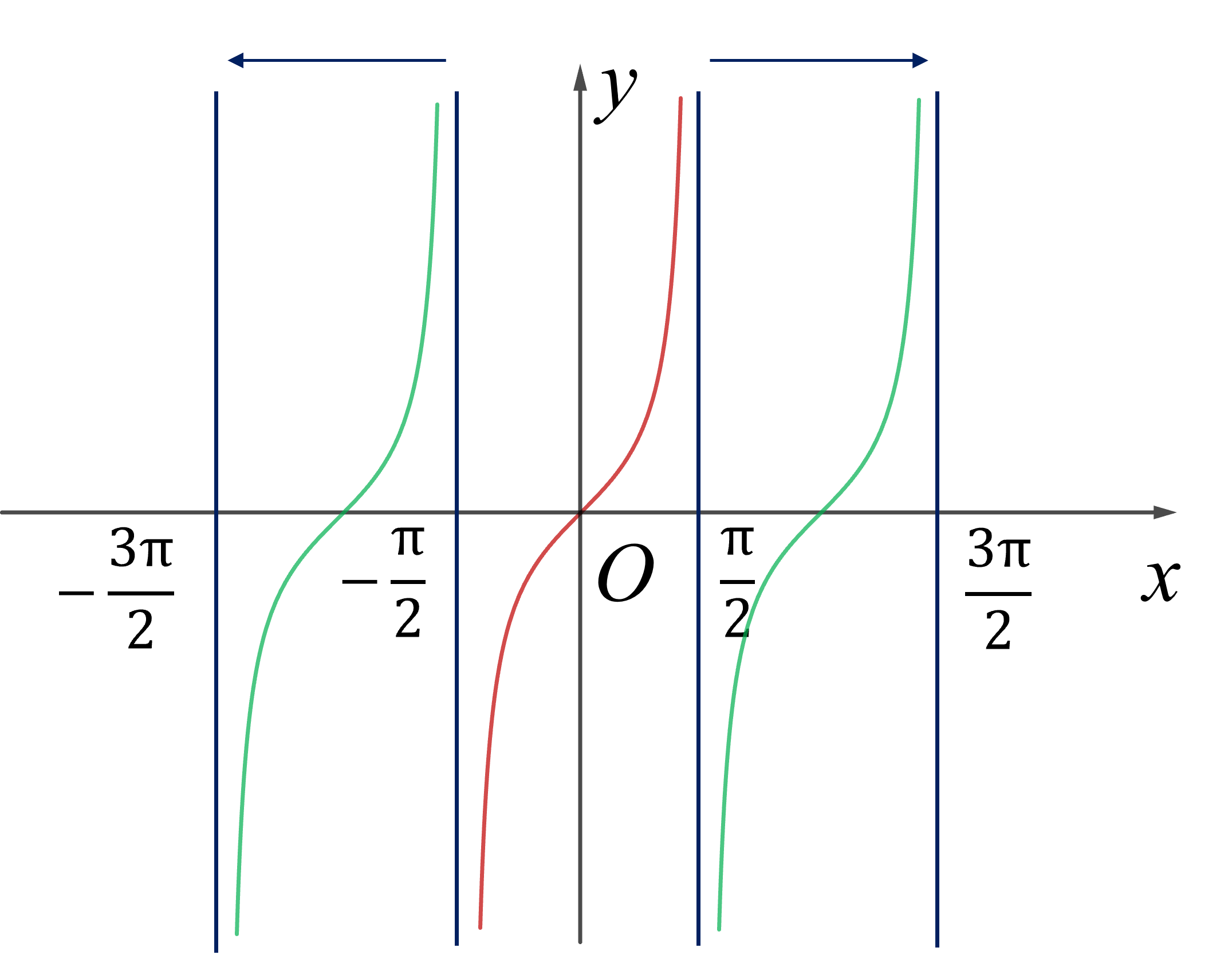
(Với mỗi giá trị $x$ đặt tương ứng với một giá trị $f(x)=\tan x$.)
1. Tập xác định của hàm số:
Do $\tan x=\dfrac{\sin x}{\cos x}$
Điều kiện xác định: $\cos x \neq 0$ hay $x \notin \{ \dfrac{\pi}{2}+k\pi \}$ ($k \in \mathbb Z$).
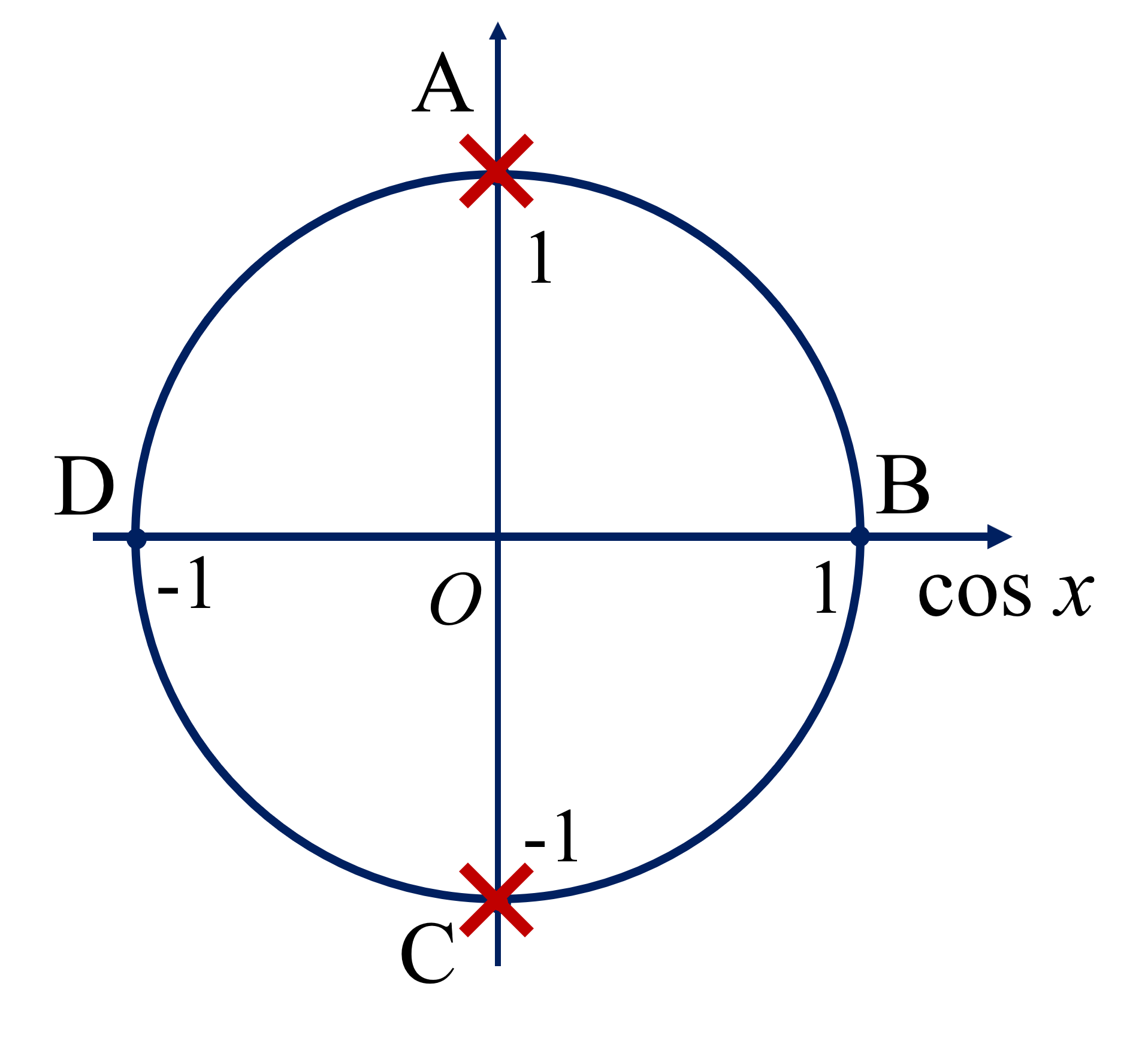
Vậy tập xác định $\mathbb D = \mathbb R$ \ $\{ \dfrac{\pi}{2} + k \pi \}$
$=...\Big( -\dfrac{3\pi}{2}; -\dfrac{\pi}{2} \Big) \cup \Big( -\dfrac{\pi}{2}; \dfrac{\pi}{2} \Big) \cup \Big( \dfrac{\pi}{2}; \dfrac{3\pi}{2} \Big) \cup ...$
Space
2. Hàm số $f(x)=\tan x$ là hàm số lẻ vì
+) Tập xác định $\mathbb D = \mathbb R$ \ $\{ \dfrac{\pi}{2} + k \pi \}$ thỏa mãn điều kiện:
$\forall x \in \mathbb D$ thì $-x \in \mathbb D$.
+) $f(-x)=\tan (-x)=-\tan x=-f(x)$
Space
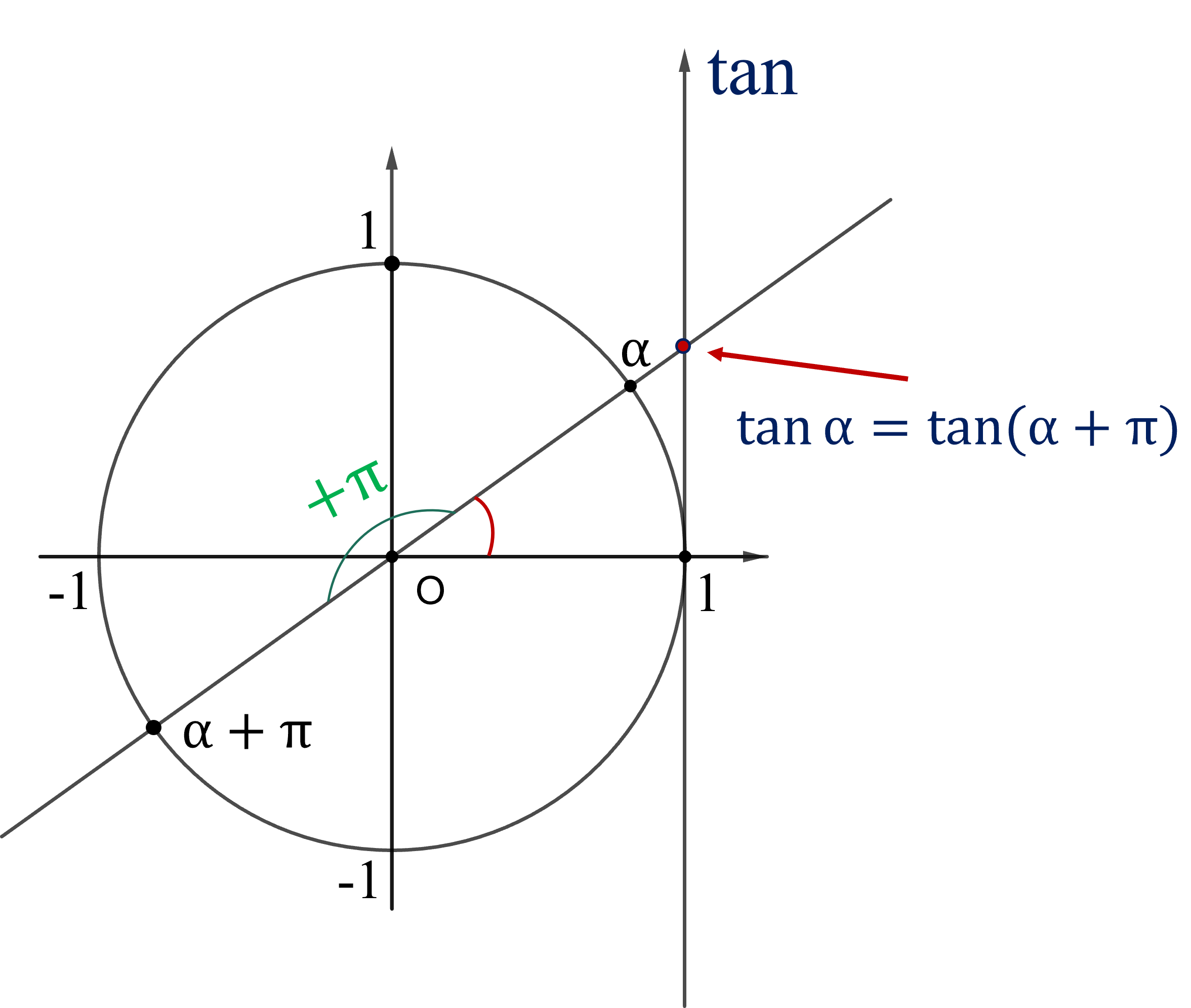
3. Hàm số tuần hoàn với chu kì $\pi$:
$\forall x \in \mathbb R;$ $\tan x=\tan (x+\pi)$
Space
4. Tính đồng biến, nghịch biến của hàm số
Hai hình vẽ dưới đây, điểm $A$ là điểm biểu diễn góc $\alpha$.
+) Khi góc $\alpha$ tăng trong khoảng $(-90^{\circ};90^{\circ})$ thì $\tan \alpha$ tăng trong khoảng $(-\infty;+\infty)$.
Xem hình minh họa:
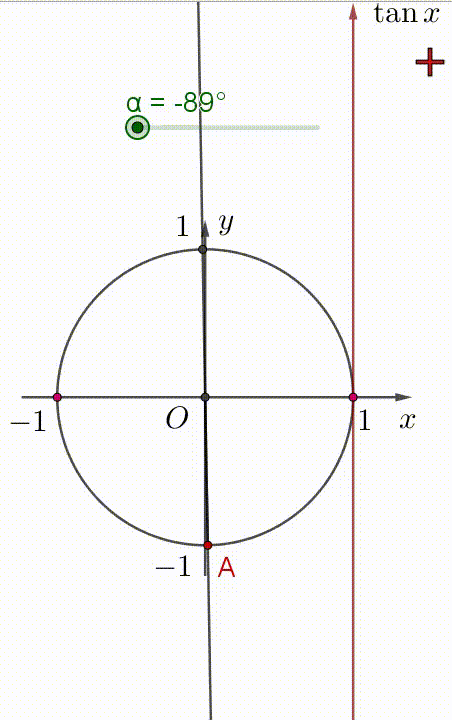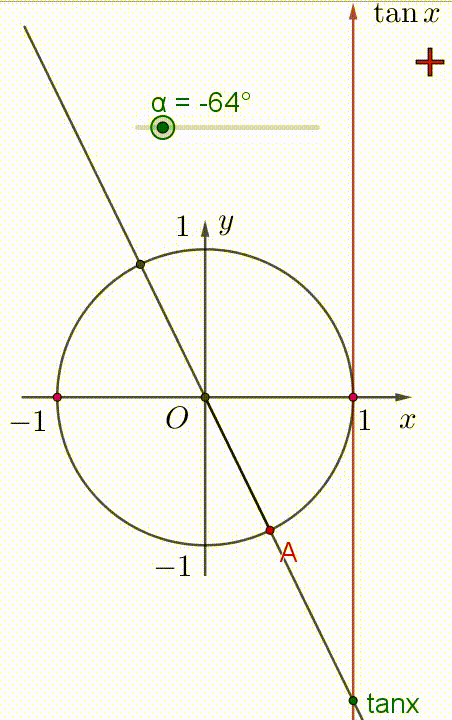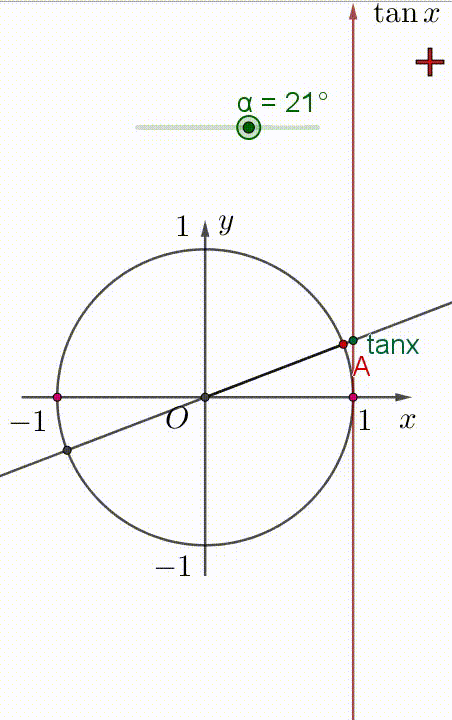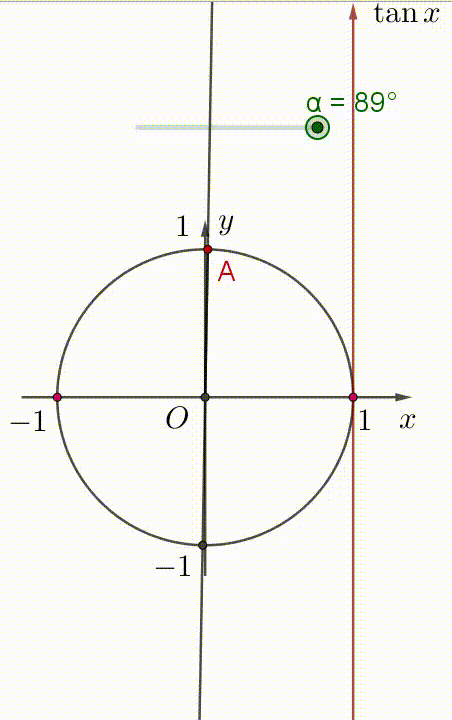
Vậy hàm số $\tan \alpha$ đồng biến trên khoảng $\Big( -\dfrac{\pi}{2};\dfrac{\pi}{2} \Big)$.
+) Khi góc $\alpha$ tăng trong khoảng $(90^{\circ};270^{\circ})$ thì $\tan \alpha$ tăng trong khoảng $(-\infty;+\infty)$.
Xem hình minh họa:
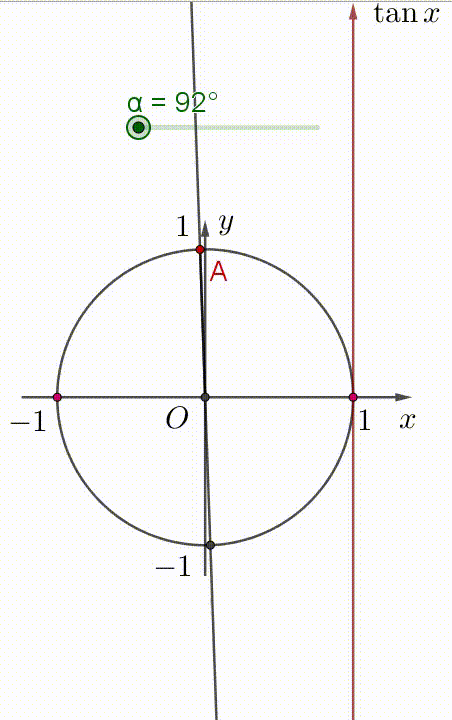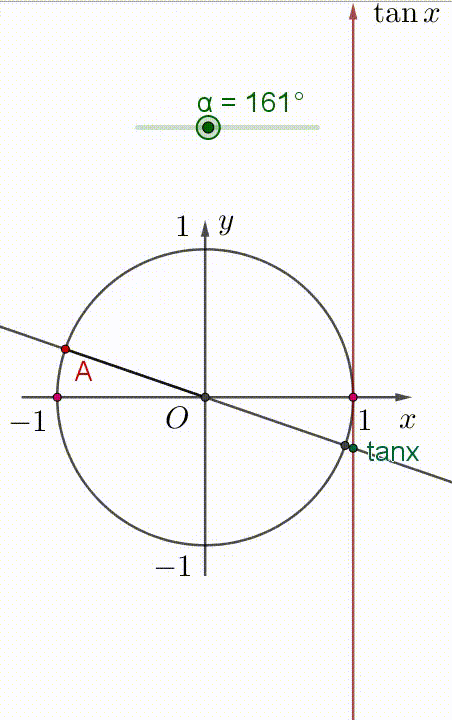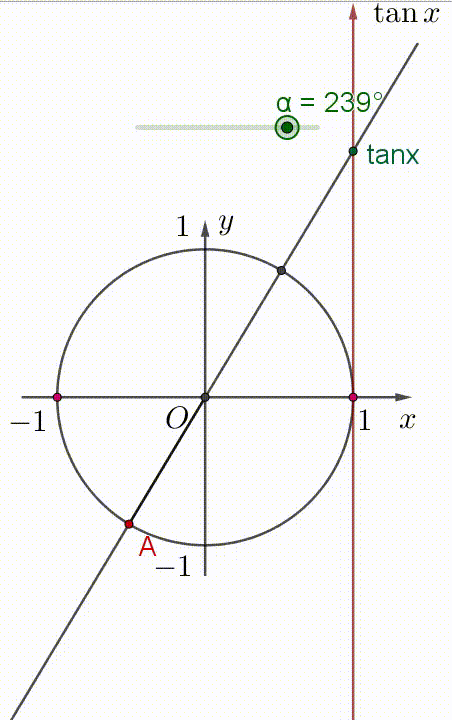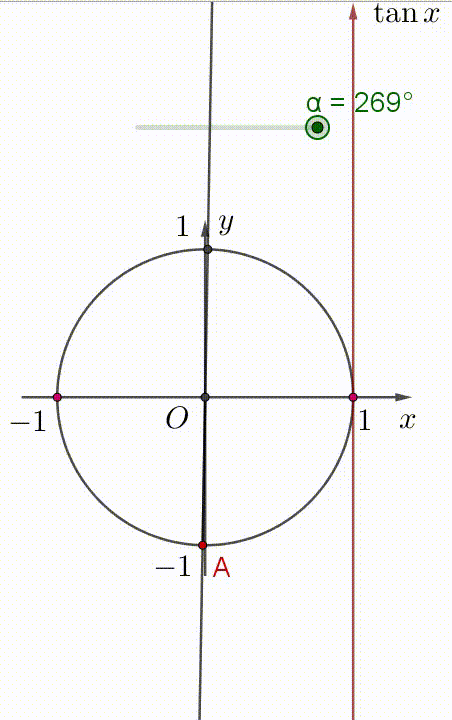
Vậy hàm số $\tan \alpha$ đồng biến trên khoảng $\Big( \dfrac{\pi}{2};\dfrac{3\pi}{2} \Big)$.
*) Kết hợp với tính tuần hoàn của hàm số, ta có kết luận, hàm số $y=\tan x$ đồng biến trên các khoảng $\Big( -\dfrac{\pi}{2}+k\pi;\dfrac{\pi}{2}+k\pi \Big)$ với $k \in \mathbb Z$.
Space
5. Vẽ đồ thị hàm số $f(x)=\tan x$.
Do hàm số $f(x)=\tan x$ có tính tuần hoàn với chu kì $\pi$ và chỉ xác định trên các khoảng $\Big( -\dfrac{\pi}{2}+k\pi;\dfrac{\pi}{2}+k\pi \Big)$ với $k \in \mathbb Z$, vậy, ta có thể vẽ đồ thị của hàm $\tan x$ trên khoảng $\Big( -\dfrac{\pi}{2};\dfrac{\pi}{2} \Big)$ sau đó dịch chuyển theo phương ngang sang trái và sang phải trên các khoảng còn lại.