Bài 3. Hàm số liên tục

I. Định nghĩa

Định nghĩa 1

Chú ý:

1. Nếu hàm số liên tục tại $x_0$ thì trước hết hàm số phải xác định tại điểm đó

2. $\lim\limits _{x \rightarrow x_0} f(x)=k \Leftrightarrow \lim\limits _{x \rightarrow x_0^{+}} f(x)=\lim\limits _{x \rightarrow x_0^{-}} f(x)=k$

3. Hàm số $y=\left\{\begin{aligned}f(x), \text { khi } x \neq x_0 \\ g(x), \text { khi } x=x_0\end{aligned}\right.$ liên tục tại $x=x_0 \Leftrightarrow \lim\limits _{x \rightarrow x_0} f(x)=g\left(x_0\right)$

4. Hàm số $f(x)=\left\{\begin{aligned}f(x), \text { khi } x \geq x_0 \\ g(x), \text { khi } x<x_0\end{aligned}\right.$ liên tục tại điểm $\quad x=x_0 \quad$ khi và chỉ khi $\lim\limits _{x \rightarrow x_0^*} f(x)=\lim\limits _{x \rightarrow x_0^{-}} g(x)=f\left(x_0\right)$

Định nghĩa 2

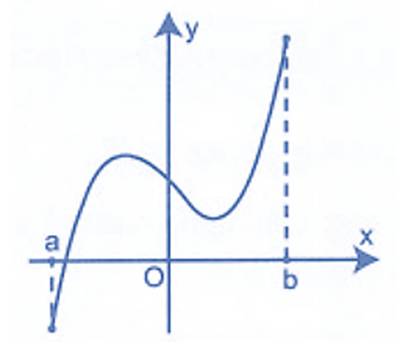
Hàm số liên tục trên khoảng $(a;b)$	Hàm số không liên tục trên khoảng $(a;b)$

Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó

II. Một số định lí cơ bản

Định lí 1

Định lí 2

Giả sử $y=f(x)$ và $y=g(x)$ là hai hàm số liên tục tại điểm $x_0$.

Khi đó

II. Các dạng bài tập

Ví dụ 1: Cho $f(x)=\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}$ với $x \neq 0$. Phải bổ sung thêm giá trị $f(0)$ bằng bao nhiêu thì hàm số liên tục tại $x=0$ ?

Giải

$\begin{aligned}\lim _{x \rightarrow 0} f(x) & =\lim _{x \rightarrow 0} \dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim _{x \rightarrow 0} \dfrac{x+2-2+x}{(\sqrt{x+2}+\sqrt{2-x})} \\& =\lim _{x \rightarrow 0} \dfrac{2}{(\sqrt{x+2}+\sqrt{2-x})}=\dfrac{1}{\sqrt{2}} .\end{aligned}$

Ví dụ 2: Xét tính liên tục của hàm số  $f(x)= \begin{cases}\dfrac{x^2-4}{x+2} & \text { khi } x \neq-2 \\ -4 & \text { khi } x=-2\end{cases}$sau trên tập xác định của nó.

Giải

Hàm số $f(x)$ liên tục với $\forall x \neq-2$
- $\lim\limits _{x \rightarrow-2} f(x)=\lim\limits _{x \rightarrow-2} \dfrac{x^2-4}{x+2}=\lim\limits _{x \rightarrow-2} \dfrac{(x+2)(x-2)}{x+2}=\lim\limits _{x \rightarrow-2}(x-2)=-2-2=-4$.
- $f(-2)=-4 \Rightarrow \lim\limits _{x \rightarrow-2} f(x)=f(-2) \Rightarrow f(x)$ liên tục tại $x=-2$
- Từ (1) và (2) ta có $f(x)$ liên tục trên $\mathbb{R}$.