Bài 15: Hàm số

1. KHÁI NIỆM HÀM SỐ

Nếu với mỗi giá trị của \(x\) thuộc tập hợp số \(D\) có một và chỉ một giá trị tương ứng của \(y\) thuộc tập số thực \(ℝ\) thì ta có một hàm số.

Ta gọi \(x\) là biến số và \(y\) là hàm số của \(x\).

Tập hợp \(D\) gọi là tập xác định của hàm số.

Tập tất cả các giá trị \(y\) nhận được gọi là tập giá trị của hàm số.

Chú ý:

• Khi \(y\) là hàm số của \(x\), ta có thể viết \(y=f\left(x\right),y=g\left(x\right),...\) 
• Khi cho hàm số bằng công thức \(y=f\left(x\right)\) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực \(x\) sao cho biểu thức \(f\left(x\right)\) có nghĩa.

Ví dụ. Tìm tập xác định của các hàm số sau:

a) \(y=\sqrt{5-3x}\);               b) \(y=\dfrac{3}{x+4}\).

Giải

a) Biểu thức \(\sqrt{5-3x}\) có nghĩa khi \(5-3x\ge0\), hay \(x\le\dfrac{5}{3}\).

Vậy tập xác định của hàm số đã cho là \(D=(-\infty;\dfrac{5}{3}].\)

b) Biểu thức \(\dfrac{3}{x+4}\) có nghĩa khi \(x+4\ne0\), hay \(x\ne-4\).

Vậy tập xác định của hàm số đã cho là \(D=\mathbb{R}\setminus \left \{ -4 \right \}\).

Nhận xét. Một hàm số có thể được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc bằng mô tả.

2. ĐỒ THỊ CỦA HÀM SỐ

Đồ thị của hàm số \(y=f\left(x\right)\) xác định trên tập \(D\) là tập hợp tất cả các điểm \(M\left(x;f\left(x\right)\right)\) trên mặt phẳng tọa độ với mọi \(x\) thuộc \(D.\)

Ví dụ.

• Đồ thị hàm số \(f\left(x\right)=x+1.\)

• Hàm số \(g\left(x\right)=\dfrac{1}{2}x^2.\)

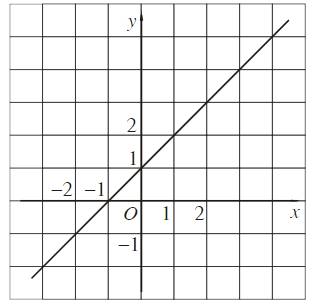
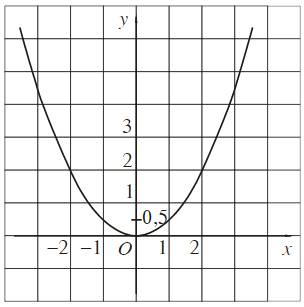
3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

Hàm số \(y=f\left(x\right)\) được gọi là đồng biến (tăng) trên khoảng \(\left(a;b\right)\) nếu:

\(\forall x_1,x_2\in\left(a;b\right),x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right).\)

Hàm số \(y=f\left(x\right)\) được gọi là nghịch biến (giảm) trên khoảng \(\left(a;b\right)\) nếu:

\(\forall x_1,x_2\in\left(a;b\right),x_1< x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right).\)

Chú ý. 

• Đồ thị của một hàm số đồng biến trên khoảng \(\left(a;b\right)\) là đường "đi lên" từ trái qua phải.
• Đồ thị của một hàm số nghịch biến trên khoảng \(\left(a;b\right)\) là đường "đi xuống" từ trái qua phải.

Ví dụ. Hàm số \(y=-2x+1\) đồng biến hay nghịch biến trên \(ℝ\).

Giải

Xét hai số bất kì \(x_1,x_2\inℝ\) sao cho \(x_1< x_2.\)

Ta có \(x_1< x_2\Rightarrow-2x_1>-2x_2\Rightarrow-2x_1+1>-2x_2+1\)

hay \(f\left(x_1\right)>f\left(x_2\right)\).

Vậy hàm số đã cho nghịch biến trên \(ℝ\).